Disclaimer! The graph theory described here is simplified and does not cover the whole topic. What you can find here helps me to build up some level of understanding of graphs for processing them.

The majority of the information here comes from The Algorithms 4th edition book.

Graph

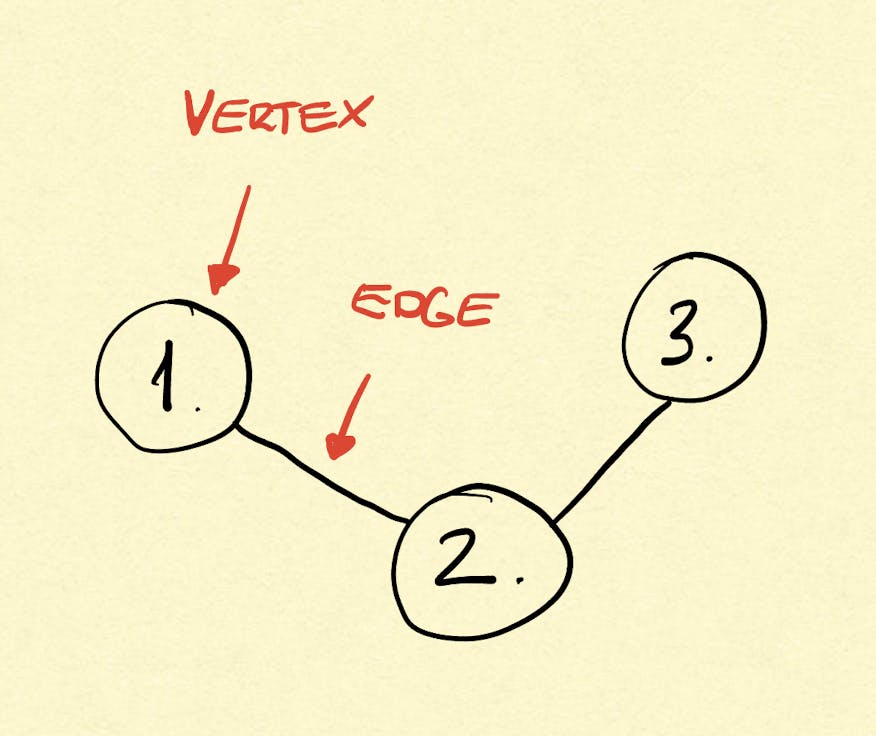
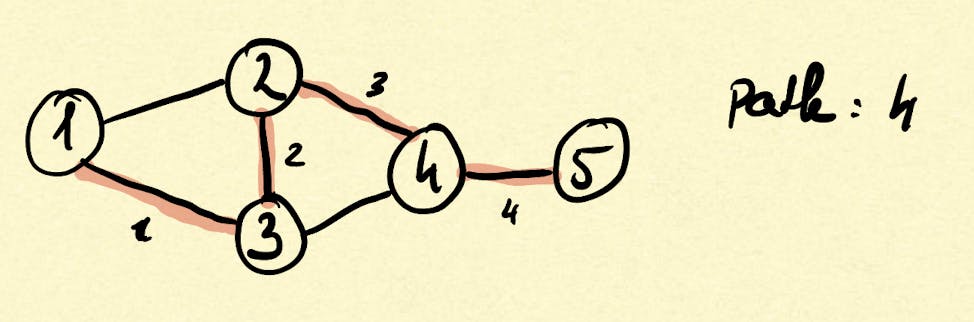
The graph is a set of vertices and a collection of edges that each connect a pair of vertices. The screenshot below shows a simplified example of this.

Definitions

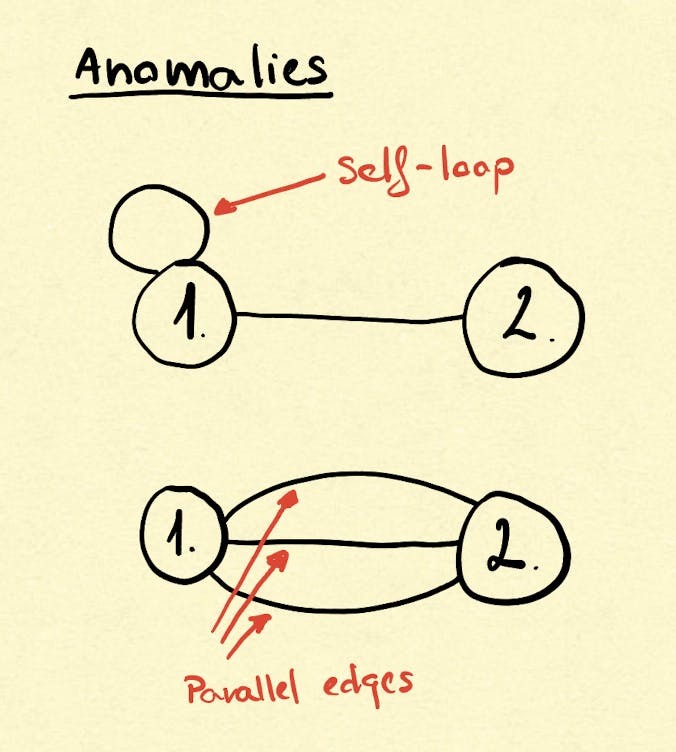
When an edge connects to a vertex to itself it is a self-loop. When two edges connect the same set of vertices we are talking about parallel edges.

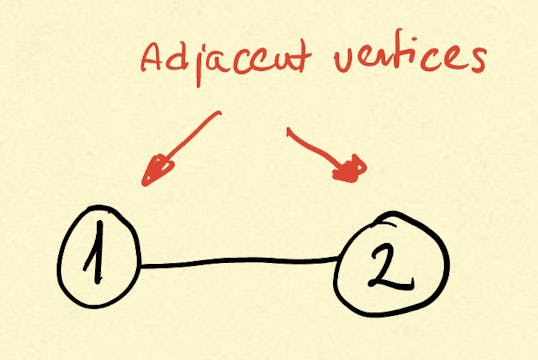
When an edge connects two vertices the vertices are adjacent to the one another and the edge is incident on both vertices.

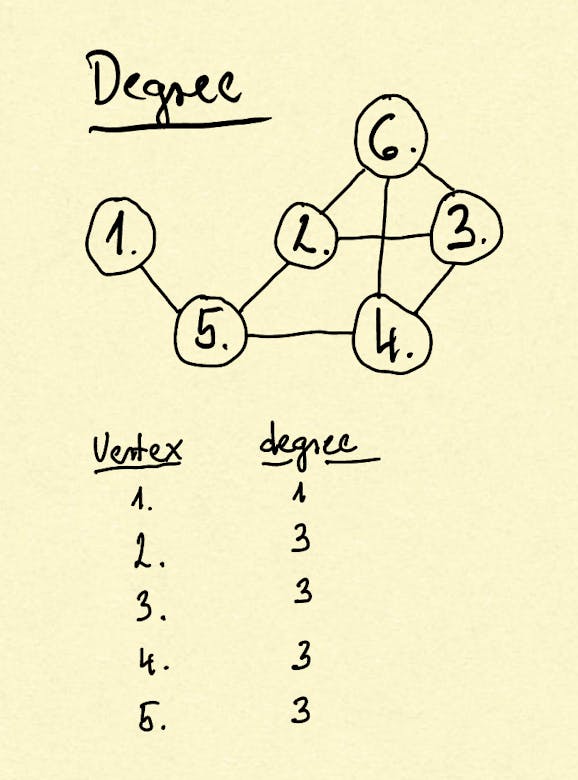
Vertices have degree property which indicates how many edges incident to it.

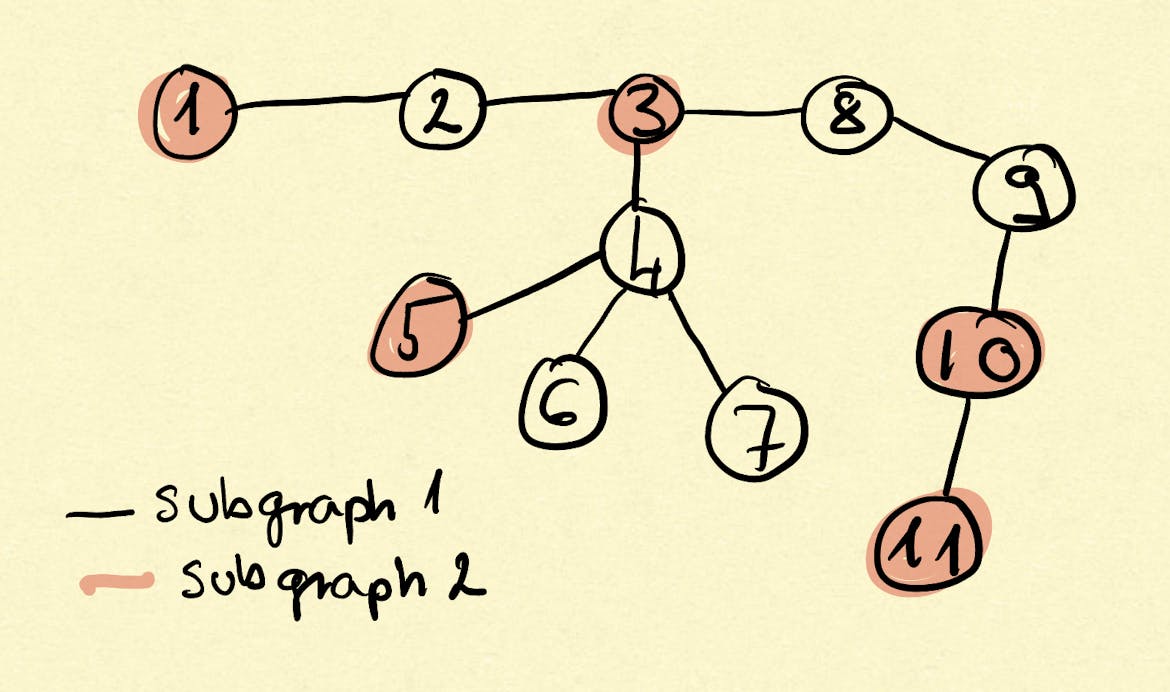
The subgraph is the subset of edges, with their vertices, that constitutes a graph.

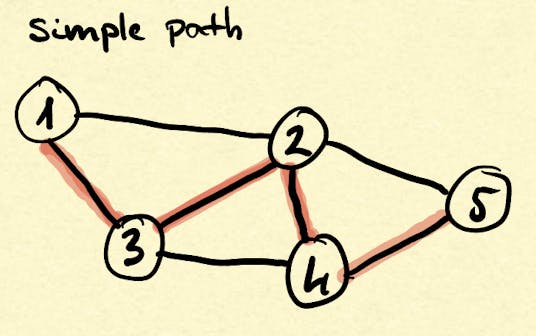
The path is a sequence of edges connected by vertices, while the simple path is when there are no repeated vertices in a path.

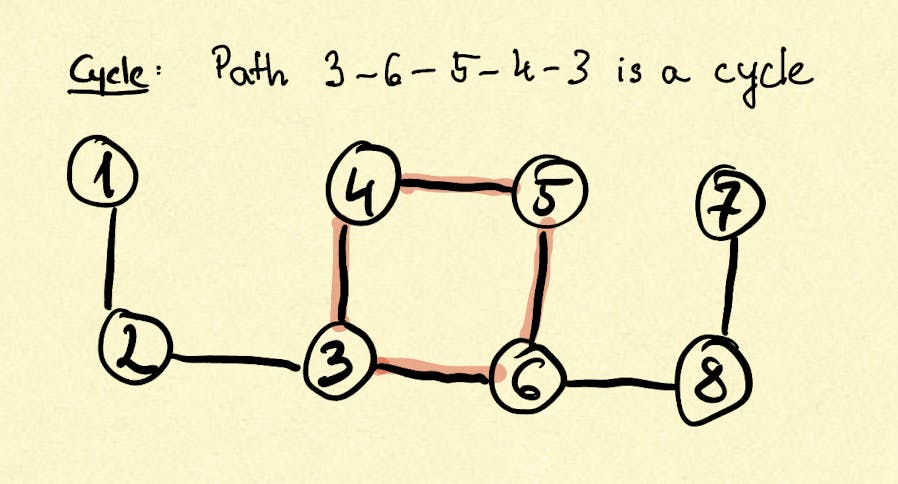
Graphs may have cycles, which is a special case of a path, where the path's first and last element is the same vertex.

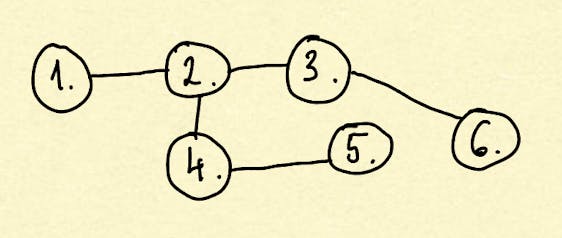
A graph that doesn't have a cycle is acyclic.

A path has a length which is the number of edges.

Connected vertices

A vertex is connected to another if there is an edge between them.

Note: this definition considers a connection between two vertices. Nothing more.

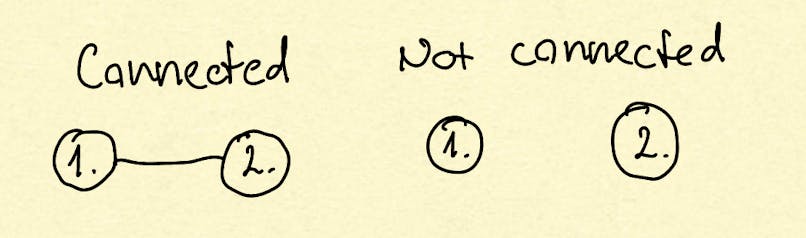
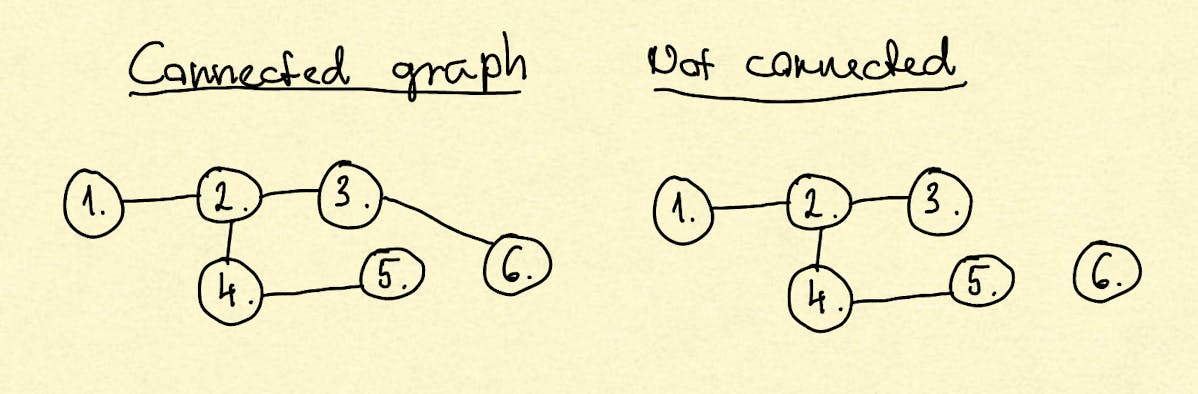
Connected graph

A graph is connected if there is a path to all vertices in the graph.

Note: this definition considers a graph and that there is a path to all vertices in the graph.

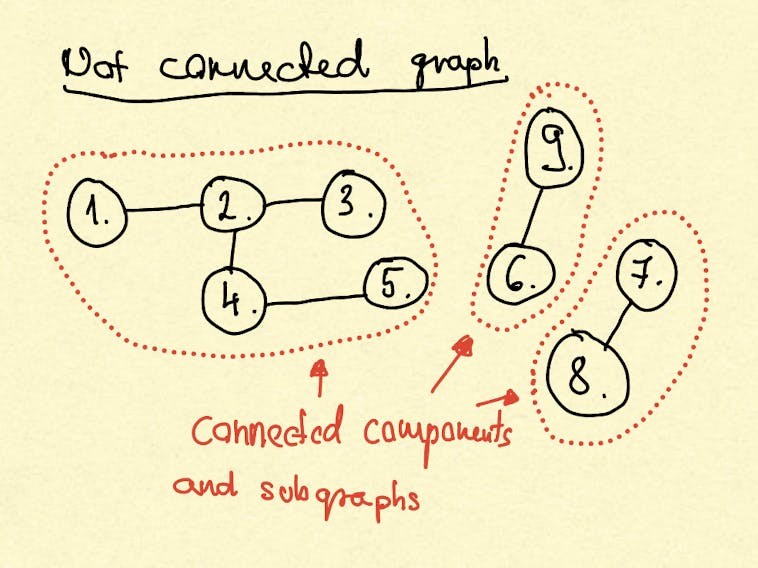
When a graph is not connected it consists of connected components. The number of connected components also indicates the maximum of how many subgraphs that constitute the graph.

Trees are special graphs meaning a tree is an acyclic-connected graph.

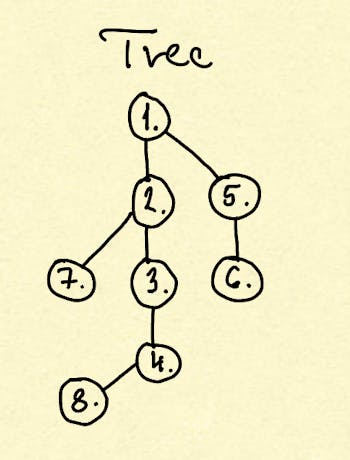
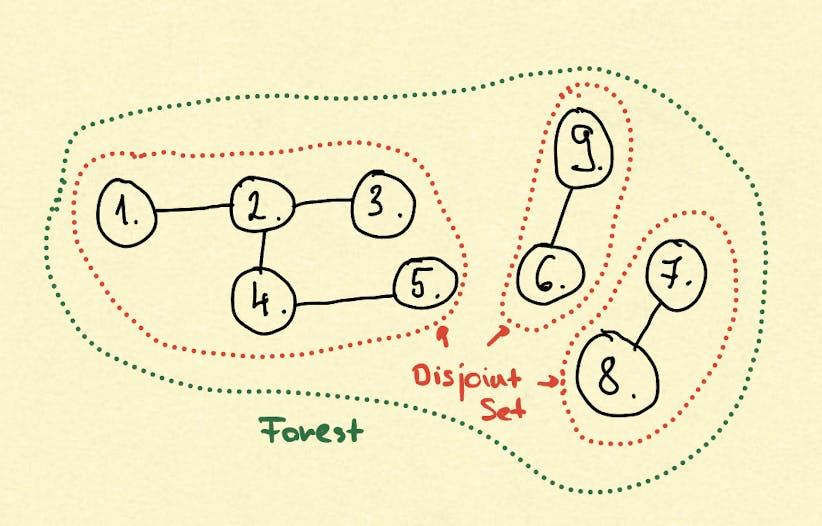
We are talking about a forest where we have disjoint sets of trees.

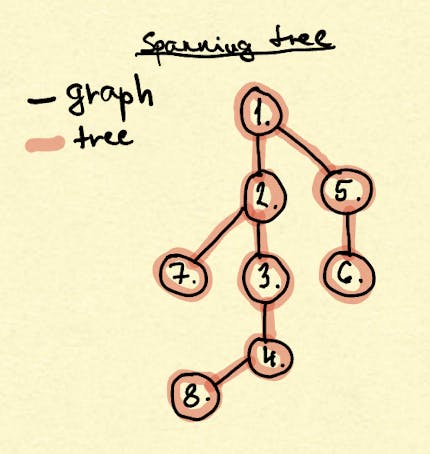
A spanning tree is a subgraph of a connected graph that includes all the vertices of the graph and also a single tree. Remember, a tree is a connected-acyclic graph.

The spanning forest of a graph is the union of spanning trees of the graph's connected components.

The bipartite graph is a graph whose vertices and edges can be divided into subgraphs where all vertices of one subgraph are connected to the other subgraph vertices.