Andras Csanyi

Data Structures: Hash table

Andras Csanyi's photo
Andras Csanyi
·

8 min read

Table of contents

Introduction

We are going to take a look at the hash table data structure. This look will only scratch the surface of the topic, so, please do a favour for yourself and read through the linked materials for better and deeper understanding.

Hash table is a data structure where the elements get an index and this index is used to put them into an array under the index they have. As a result adding an element to an hash table will be theoretically O(1) and retrieving this element also will be theoretically O(1). Hash table provides the index calculation which called hashing. Adding and retrieving an element from a hash table is O(1) + hash calculation cost.

Hash table is a time-space complexity trade-off. In this case we trade hash calculation cost for faster access. The alternative would be a sequential search in an array or linked list where we put our elements. [1]

Goal

As I mentioned in the previous section one part of the goal is to put the any type of elements in some order, where to find any element takes a reasonable time. Reasonable means in that case that it is faster than arrays, linked lists O(n) property.

The other part of the goal is that the solution should provide a reasonable space complexity too. It means, it should not be significantly more than of an array or linked list.

How hash table works

Add

When you add a new value to a hash table the following steps will be executed:

  1. the value you added will be hashed, meaning an integer value will be calculated
  2. the hash table internal logic checks if the key already occupied or not. If there is a collision, then it will be resolved and the value added. If there is no collision, then it adds the value to the internal data structure.

Retrieve

When an element is retrieved from the hash table the following steps will be executed:

  1. the value will be hashed, meaning an integer value will be calculated
  2. the hash table implementation checks whether the given key is subject of collision resolution or not. If so, then the hash table implementation finds the right value and returns with it. If there is not collision it just returns the value.

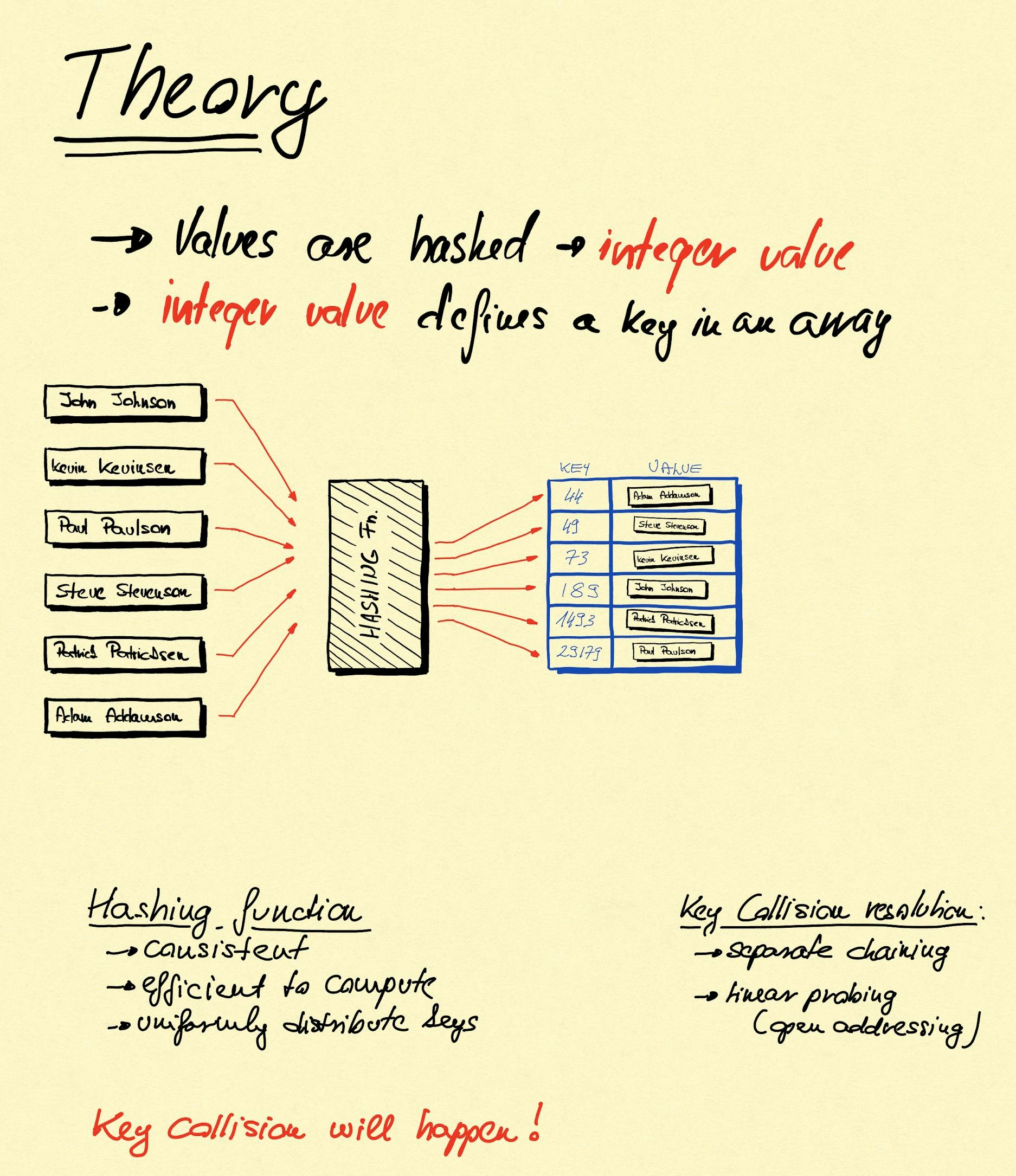
Screenshot 2022-08-21 at 14.01.49.jpg

Hashing

Dead simple explanation

Take the value you want to add to the hash map and make a hash from it. Meaning, you'll get an integer value which defines the index value in an array it will be placed.

A bit more detailed explanation

We already know that if we know the index of an array element then we have O(1) read/write access to it. Somehow this integer value needs to be produced. Hashing is the operation where the value we want to work with is used as base of creating an integer value. This operation is called hashing.

There are interesting questions when it comes to hashing:

  • how integer values are generated from different types like integer, boolean, string and especially user created types?
  • Is the hashing method is out-of-box or has to be implemented?
  • what is the cost of hashing? Does it make the code slower?
  • what if when two different value results the same hash value?

How hash values are generated

In general, every programming language which offer some implementation of hash map, dictionary or associative array provides solution for being able hash anything. So, we don't have to deal with it.

The Algorithms book discusses an easy to understand detail how hashes are generated. Worth to read [2] or watch the video course. [3]

My recommendation is that you should take a look at it to have some level of understanding what is happening.

Expectations of hashing[4]:

  • it should be consistent - equals keys must always produce the same hash value
  • it should be efficient to compute
  • it should uniformly distribute the set of keys[5]

Speed of hash functions

The hash implementations programming languages provide are good enough for general cases.

Collisions

Key collision will happen and there are collision resolutions methods helping us to deal with it.

Collision resolution

There are multiple solution exist to manage the case when two distinct values result in the same hash value.

Please note that, collision resolution is also a thing you don't have to deal with since the programming language you are using provides solution for this. However, it is good to be familiar with the problem space.

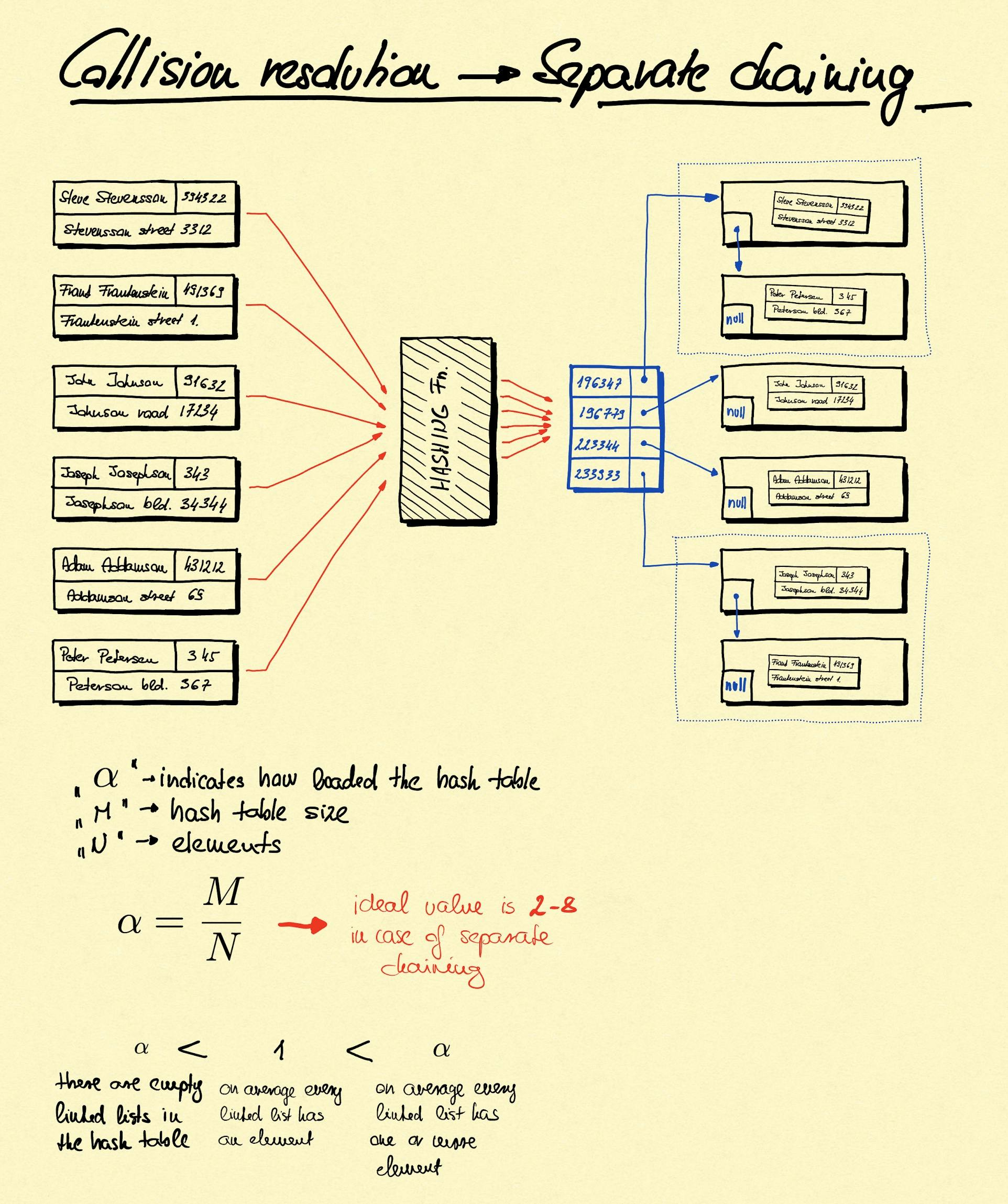
Separate chaining

Separate chaining is the solution for the case when two values get the same hash value and the hash table internal logic resolves this case by putting them into a singly linked list. This solution assumes that eventually these linked lists will be short (a few items only), so the O(n) nature of searching in a linked list won't be a significant overhead.

In this case an important factor the array size (AS) and the amount of elements (AE). If AS is significantly greater than AE we can be sure of that only little amount of values will be hashed to the same value (see uniformly distributed expectation). As a result the extra overhead of searching in a linked list, which is O(n) is very little.

In case of separate chaining AS/AE (called "alpha") is bigger than 1 meaning that on average every linked list has a single element. In case of separate chaining ideal value for "alpha" is between 2-8. If "alpha"s value is growing above the ideal value then hash table resizing comes into picture. See it later.

Further discussions can be found here [6].

Screenshot 2022-08-21 at 14.03.54.jpg

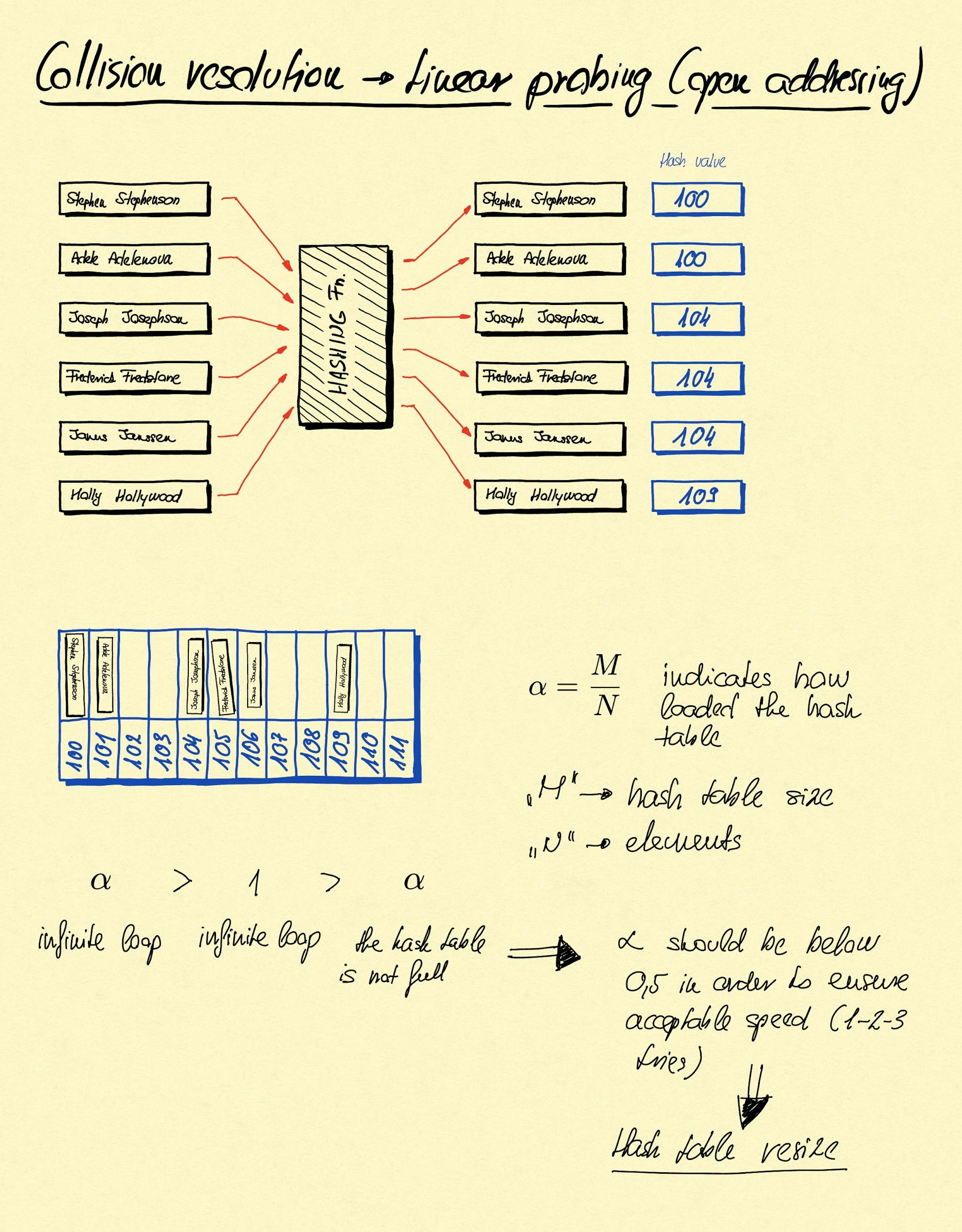
Open addressing - linear probing

Open addressing is another solution for the key collision problem. In this case when a collision happens we use the next available index in the array to store the value.

In the added drawings you can see the following:

  • we have the values at the left side ("Stephen Stephenson" and friends)
  • when they are hashed they get the hash values marked in the right side in a blue box. This value determines under which index the values will be inserted in the blue array somewhere in the middle of the page
  • let's insert "Stephen Stephenson", this element got the "100" hash value, so it will be inserted under the index "100" in the array
  • let's insert "Adele Adelenova", this element also got the "100" hash value, so it should be inserted under the key "100", but it is already occupied. The linear probing algorithm in this case checks whether the next element, in this case "101" is available or not. It is available, so the "Adele Adelenova" object will be inserted there
  • let's insert "Joseph Josephson", this element got the "104" hash value, so it should be inserted under the key "104". It is available, so will be inserted there.
  • let's insert "Frederick Fredstone", this element also got the "104" hash value, so it should be inserted under the key "104", but it is not available. The internal logic of hash table checks whether the next index is available or not. It is available, so it inserts there.
  • the case is the same with "Janus Janssen"

Screenshot 2022-08-21 at 14.19.25.jpg

In case of searching the same happens but backwards.

In this solution "alpha"'s value is important, which is computed like follows: $$ \alpha = N/M $$ where N == amount of values will be inserted, and M == hash table size.

As alpha gets closer to 1 the higher the chance of clusters building up (in our example above the index "104, "105", and "106" creates a cluster), and insert and search operations takes longer and longer time since the internal logic has to step to the next index and checks the value there. As alpha reaches 1 there will be an infinite loop since once the internal logic reaches the end of the array it will jump to the first element and continues the search. If alpha value kept around 1/2 then it can be ensured that every insert and search operation takes 1-2-3 probes to find or place the value. [7]

Size management

As we could see in the previous sections when hash table uses linear probing for collision resolution it is important to keep alpha value around 1/2. In case of separate chaining this value is between 2-8. In order to achieve that size management functionalities can be added to the hash map implementations.

Resizing is when the hash map internal array size is increased and all the values already stored in the hash map are rehashed again. This is similar to what dynamic size array does meaning the whole structure is recreated. The once in a while resizing operation and the cost coming with it seems to be acceptable in order to keep insert and search operations fast enough. [8]

Ordering

If you need ordering among the values stored in hash table, then hash table is not the right solution for that.

References

Links

hash tablealgorithmsdata structures