Data Structures: (Doubly) Linked List
I fill up the holes in my knowledge regarding data structures and in this article a write up what I have learned about Doubly Linked Lists. I’m happy if you use this material, but please do a favour for yourself and don’t accept fully what you find here. Read through the sources to get a full picture.
Doubly Linked List is another data structure where we can shovel stuff into a sequential order. Even though it sounds like the array it differs significantly. Moreover, the doubly linked list tackles with the problem of traversing backward in the singly linked list is difficult.
First we have to mention that doubly linked list consists of nodes. A node, in case of doubly linked list, contains at least three properties, one for the value we would like to store in the sequence, the other two are pointers, one points to the previous and the other one to the next element in the sequence.
In Linked List the nodes are stored in sequential order and every node has a pointer to the next node and another pointer to the previous node. See the figure below. If we take a look at how these nodes are stored in the memory we see that Linked List doesn’t require contiguous memory. Nodes of linked list may be scattered across the whole memory. (In reality they aren’t because there is a language runtime which has its own dedicated memory and within that the nodes might be scattered across the memory, but this is an implementation detail, if I may.) This way of storing elements makes possible the following:
when you create a linked list its size doesn’t have to be defined,
when a new item is added to the list size management, like we saw in case of arrays, is not necessary
more effective memory usage
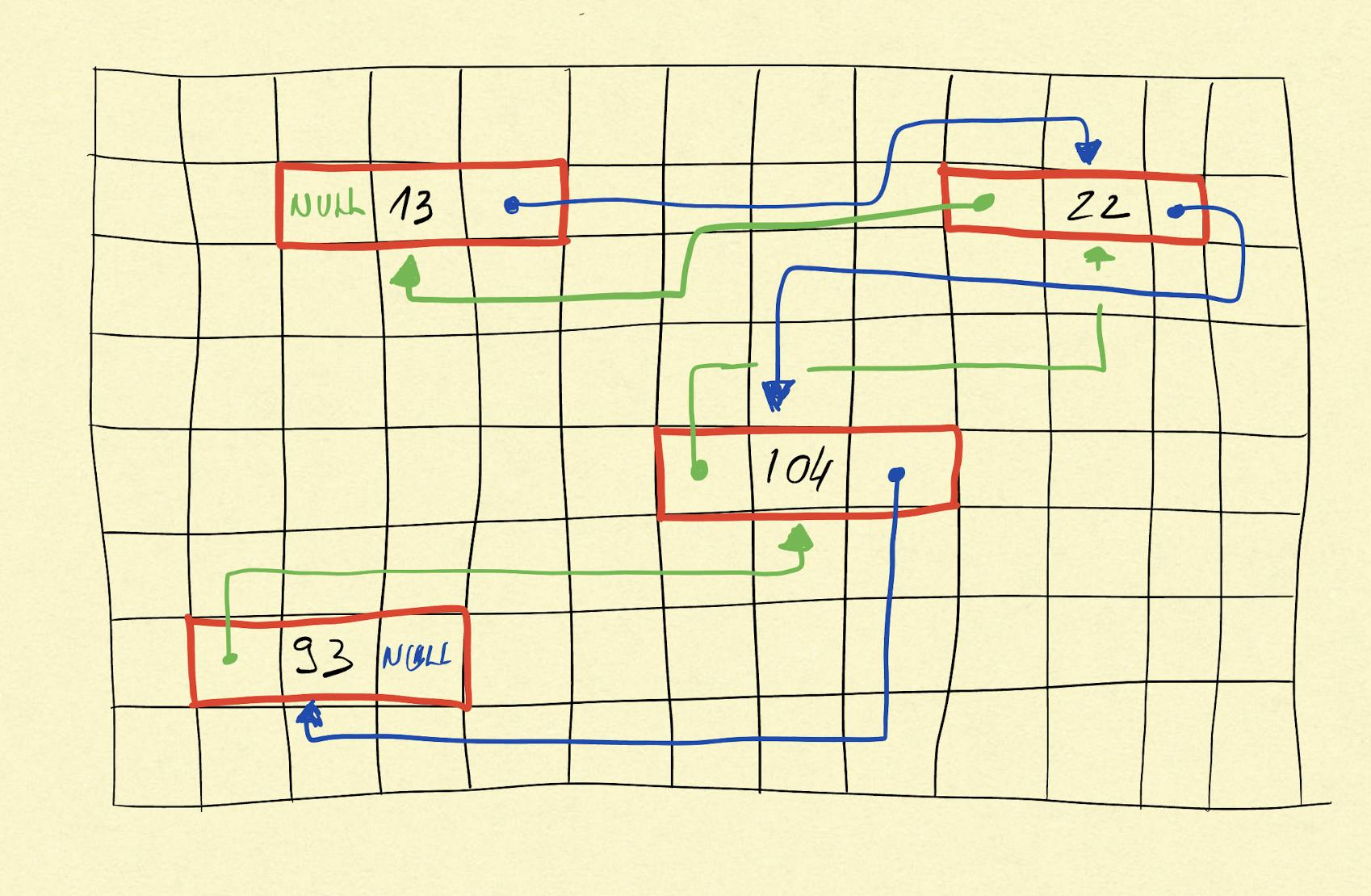
The screenshot below shows how a doubly linked list with 4 elements is stored. A red rectangle is a node which has value (“13”), and pointer to the next node (blue lines) and another pointer to the previous node (green line). Please note that the representation of the memory allocation here is conceptual only, no bits, bytes and data types are considered here.
Node with value “13” is the head as it is the first in the sequence as it doesn't point to a previous node.
Node with value “22” has two pointers, one of them points to previous node value with "13", and the other one points to the node with "104" which is the next node.
Node with value “93” is the tail, as it doesn’t have a pointer pointing to the next node, but has a pointer to the previous node.
Operations and Big O
+-----------------+-------+
| Operation | Big O |
+-----------------+-------+
| Add | O(1) |
| Delete | O(1) |
| Search/Traverse | O(n) |
| Update | O(1) |
+-----------------+-------+
Add → O(1)
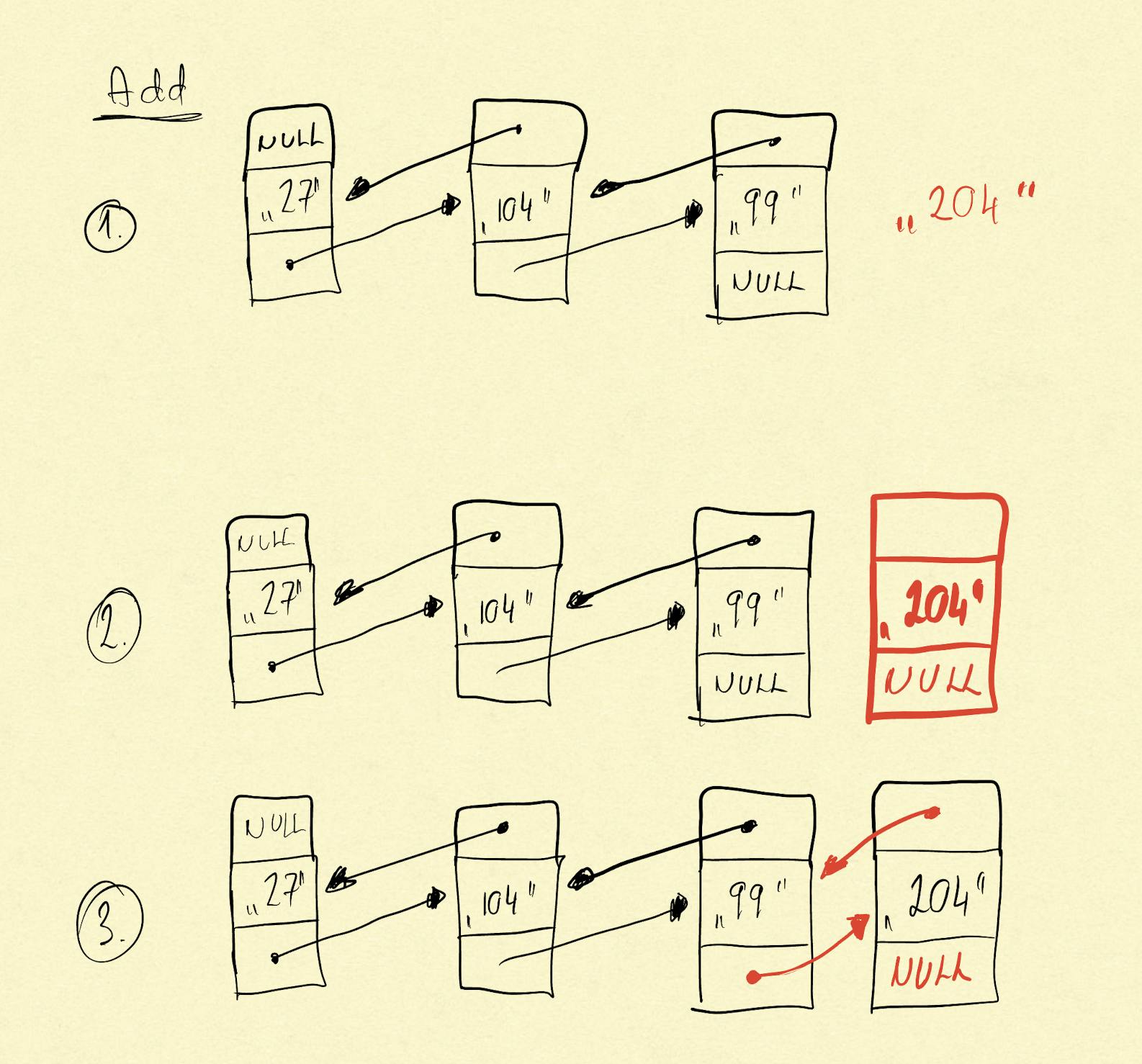
This operation adds a new element to the end of a doubly linked list. The drawings below describes that:
we have the value “204” which should be stored in the linked list — step 1
a new node is created — step 2,
its data property is set up to the value we want to store — step 2,
the previous node reference points to the new item — step 3,
the new node previous node reference points to the previous node -- step 3
the new node’s reference to the next item is null since there is no new item — step 3
As you can see adding a new node to the list doesn’t include any size management like we saw in case of arrays.
Important to note that Add operation doesn’t include finding the element which after we add the new node.
Before we move on I have to emphasise that inserting a new node anywhere in Linked List is also O(1). This is a huge advantage over array (remember, size management: copy array content and allocating contiguous memory) especially when there is an operation with lot of list merging operation. There will be another article about when to use array and when to use linked list.
Delete → O(1)
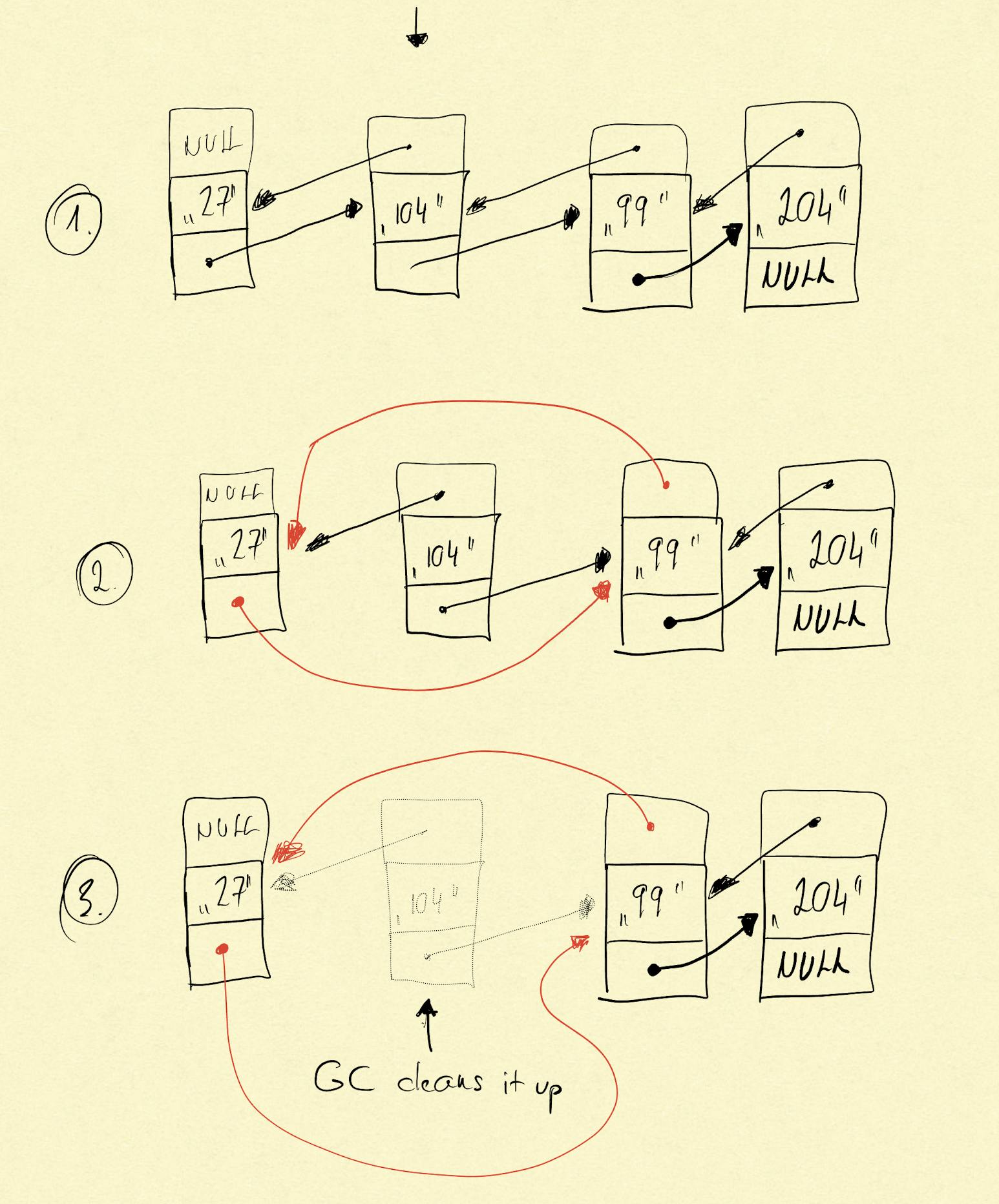
This operation removes a node from the linked list. The drawing below describes the following steps:
we have a linked list which from we want to delete node with value “104” — step 1
the node with value “27” has a reference to the node with value “104” and this reference is changed, so it points to node with value “99” — step 2
the node with value "99" has a reference to the node with value "104" and this reference is changed, so it points to node with value "27" -- step 2
the node we want to delete can be deleted (in case of C# it means the garbage collector cleans it up since no reference to it) — step 3
As you can see deleting a node from linked list doesn’t include any size management like we saw in case of arrays.
Important to note that Delete operation doesn’t include finding the node we want to delete.
Search/Traverse → O(n)
This operation is about finding a node in the linked list. Finding the value we are looking for we have to iterate through the linked list and compare each node value. In a perfect situation in might be the first one, but in worst case it is the last one.
Update → O(1)
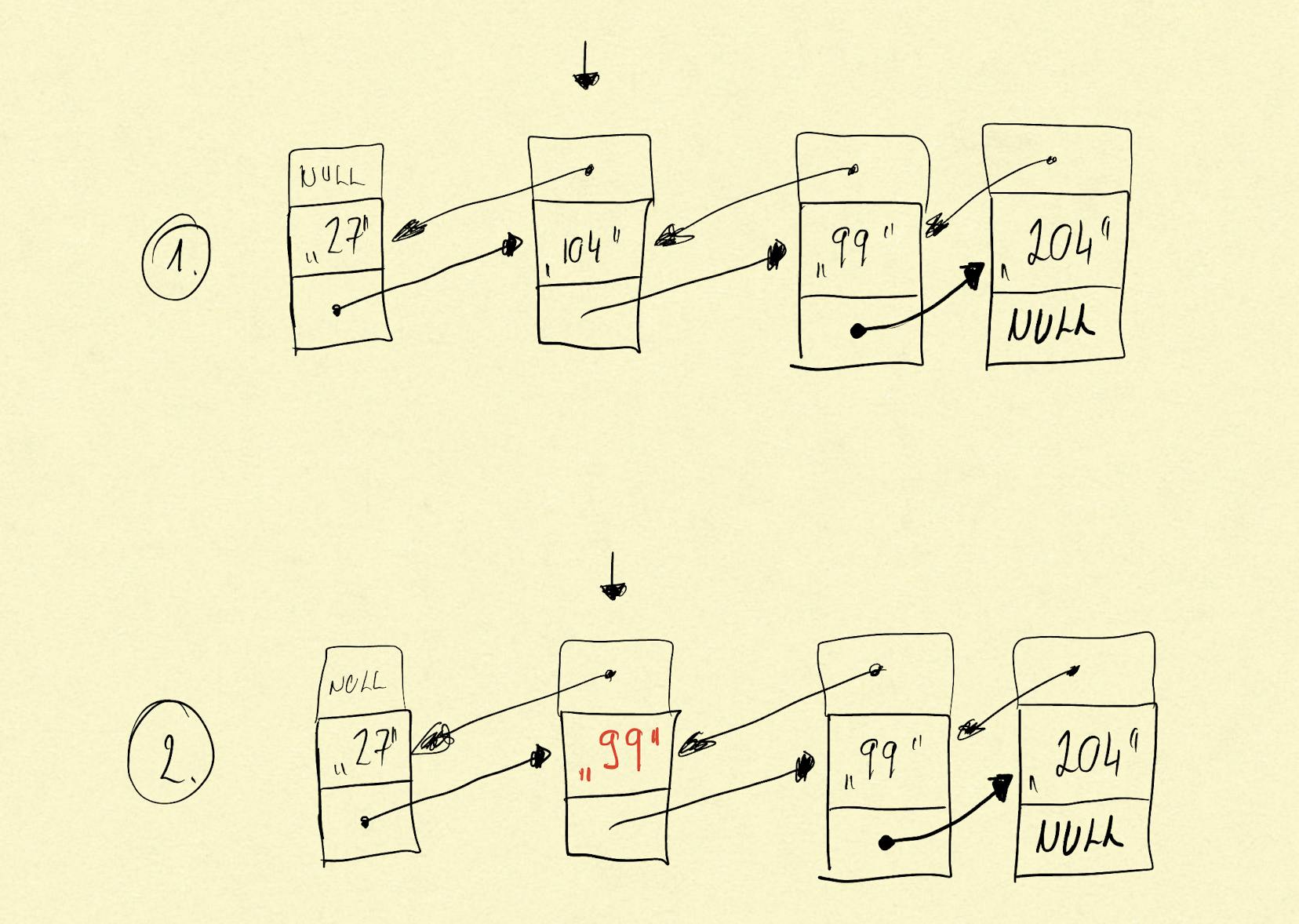
Update operation changes the node value. In order to achieve this we only have to update the node value with the new value. The screenshot below describes the process of updating a node value:
we have a linked list where we would like to change the value of the node with value “104” — step 1
the node value is overwritten to value “99”, no pointers changed in the linked list — step 2
Important to note that Update operation doesn’t include finding the node we want to update.
